3.2 The Derivative as a Function
In the previous section, we computed the derivative \(f(a)\) for specific values of \(a\). It is also useful to view the derivative as a function \(f'(x)\) whose value at \(x = a\) is \(f'(a)\). The function \(f'(x)\) is still defined as a limit, but the fixed number \(a\) is replaced by the variable \(x\):
\[f'(x) = \lim\limits_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h} \tag{1}\]
If \(y = f(x)\), we also write \(y'\) or \(y'(x)\) for \(f'(x)\).
Often, the domain of \(f'(x) \) is clear from the context. If so, we usually do not mention the domain explicitly.
The domain of \(f'(x)\) consists of all values of \(x\) in the domain of \(f(x)\) for which the limit in Eq. (1) exists. We say that \(f(x)\) is differentiable on \((a, b)\) if \(f'(x)\) exists for all \(x \in (a, b)\). When \(f'(x)\) exists for all \(x\) in the interval or intervals on which \(f(x)\) is defined, we say simply that \(f(x)\) is differentiable.
EXAMPLE 1
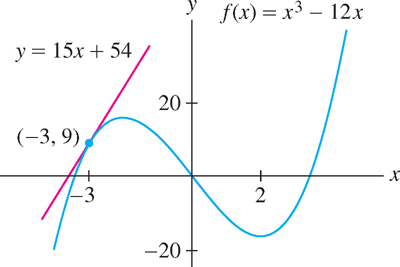
Prove that \(f(x) = x^{3} - 12x\) is differentiable. Compute \(f'(x)\) and find an equation of the tangent line at \(x = -3\).
Solution We compute \(f'(x)\) in three steps as in the previous section.
Step 1. Write out the numerator of the difference quotient.
\begin{align*}f(x+h) - f(x) & = ((x+h)^3 - 12(x+h)) - (x^3 - 12x)\\ & =(x^3 + 3x^2h +3xh^2 + h^3 - 12x - 12h)-(x^3 -12x)\\ & =3x^2h + 3xh^2 + h^3 - 12 h \\ & =h(3x^2 + 3xh + h^2 - 12)\quad(\text{factor out }h)\end{align*}
Step 2. Divide by \(h\) and simplify.
\[\frac{f(a+h)-f(a)}{h}= \frac{h(3x^2 + 3xh + h^2 - 12)}{h} = 3x^2 + 3xh + h^2 - 12\;(h\neq 0)\]
Step 3. Compute the limit.
\[f'(x)=\lim\limits_{h\rightarrow 0}\frac{f(a+h)-f(a)}{h}=\lim\limits_{h\rightarrow 0}(3x^2 + 3xh + h^2 - 12) = 3x^2 -12\]
In this limit, \(x\) is treated as a constant because it does not change as \(h\rightarrow 0\). We see that the limit exists for all \(x\), so \(f(x)\) is differentiable and \(f'(x) = 3x^{2} - 12\).
Now evaluate:
\begin{align*}f(-3)&=(-3)^{3}-12(-3) = 9\\f'(-3)&=3(-3)^{2}-12 = 15 \end{align*}
An equation of the tangent line at \(x = -3\) is \(y - 9 = 15(x + 3)\) (Figure 3.10).
130
EXAMPLE 2
Prove that \(y = x^{-2}\) is differentiable and calculate \(y'\).
Solution The domain of \(f(x) = x^{-2}\) is \(\{x : x \neq 0\}\), so assume that \(x\neq 0\). We compute \(f'(x)\) directly, without the separate steps of the previous example:
\begin{align*}y' &= \lim\limits_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h}=\lim\limits_{h\rightarrow 0}\frac{\frac{1}{(x+h)^2}-\frac{1}{2}}{h}\\ &=\lim\limits_{h\rightarrow 0} \frac{\frac{x^2- (x+h)^2)}{x^2(x+h)^2}}{h} = \lim\limits_{h\rightarrow 0} \frac{1}{h}\left(\frac{x^2- (x+h)^2)}{x^2(x+h)^2}\right)\\ &=\lim\limits_{h\rightarrow 0}\frac{1}{h}\left(\frac{-h(2x+h)}{x^2(x+h)^2}\right) = \lim\limits_{h\rightarrow 0}-\frac{2x+h}{x^2(x+h)^2} \text{ (cancel }h)\\ &=-\frac{2x+0}{x^2(x+0)^2} = -\frac{2x}{x^4} = -2x^{-3}\end{align*}
The limit exists for all \(x\neq 0\), so \(y\) is differentiable and \(y' = -2x^{-3}\).
Question 3.4 Derivative As a Function Progress Check 1
Find the derivative \(f'(x)\) for the function \(f(x) = x^2 +x-17\).
| A. |
| B. |
| C. |
3.2.1 Leibniz Notation

The “prime” notation \(y'\) and \(f'(x)\) was introduced by the French mathematician Joseph Louis Lagrange (1736–1813). There is another standard notation for the derivative that we owe to Leibniz (Figure 3.11):
\[\frac{df}{dx}\text{ or }\frac{dy}{dx}\]
In Example 2, we showed that the derivative of \(y = x^{-2}\) is \(y' = -2x^{-3}\). In Leibniz notation, we would write
\[\frac{dy}{dx} = -2x^{-3}\text{ or }\frac{d}{dx}x^{-2} = -2x^{-3}\]
To specify the value of the derivative for a fixed value of \(x\), say, \(x = 4\), we write
\[\frac{df}{dx}\Bigg|_{x=4}\text{ or }\frac{dy}{dx}\Bigg|_{x=4}\]
Thinking of \(\frac{dy}{dx}\) as a fraction forces us to confront the question: what actually are \(dy\) and \(dx\)? We cannot answer this question precisely. Leibniz thought of them as "infinitely small" changes in \(y\) and \(x\). The notation, however, proved to be so incredibly useful (especially to physicists) that in the first half of the 20th century mathematicians figured out a rigorous explanation which is now known as the theory of differential forms which you may encounter in your advanced studies.
CONCEPTUAL INSIGHT
Leibniz notation is widely used for several reasons. First, it reminds us that the derivative \(\frac{df}{dx}\), although not itself a ratio, is in fact a limit of ratios \(\frac{\Delta f}{\Delta x}\). Second, the notation specifies the independent variable. This is useful when variables other than \(x\) are used. For example, if the independent variable is \(t\), we write \(\frac{df}{dt}\). Third, we often think of \(\frac{d}{dx}\) as an “operator” that performs differentiation on functions. In other words, we apply the operator \(\frac{d}{dx}\) to \(f\) to obtain the derivative \(\frac{df}{dx}\). We will see other advantages of Leibniz notation when we discuss the Chain Rule in Section 3.7.
A main goal of this chapter is to develop the basic rules of differentiation. These rules enable us to find derivatives without computing limits.
131
The Power Rule is valid for all exponents. We prove it here for a whole number \(n\) (see Exercise 95 for a negative integer \(n\) and p. 183 for arbitrary \(n\)).
THEOREM 1 The Power Rule
For all exponents \(n\),
\[\frac{d}{dx}x^n = nx^{n-1}\]
Proof
Assume that \(n\) is a whole number and let \(f(x) = x^{n}\). Then
\[f'(a) = \lim\limits_{x\rightarrow a}\frac{x^n-a^n}{x-a}\]
To simplify the difference quotient, we need to generalize the following identities:
\begin{align*}x^2 - a^2 &= (x-a)(x+a)\\ x^3 - a^3 &= (x-a)(x^2+xa+a^2) \\ x^4 - a^4 &= (x-a)(x^3+x^2a+xa^2+a^3)\end{align*}
The generalization is
\[x^n - a^n = (x-a)(x^{n-1} + x^{n-2}a + x^{n-3}a^2+\cdots+xa^{n-2}+a^{n-1})\tag{2}\]
To verify Eq. (2), observe that the right-hand side is equal to
\begin{multline*}x(x^{n-1} + x^{n-2}a + x^{n-3}a^2+\cdots+xa^{n-2}+a^{n-1})\\-a(x^{n-1} + x^{n-2}a + x^{n-3}a^2+\cdots+xa^{n-2}+a^{n-1})\end{multline*}
When we carry out the multiplications, all terms cancel except the first and the last, so only \(x^{n} - a^{n}\) remains, as required.
Equation (2) gives us
\[\frac{x^n - a^n}{x-a} = \underbrace{x^{n-1} + x^{n-2}a + x^{n-3}a^2+\cdots+xa^{n-2}+a^{n-1}}_{n\text{ terms}}\quad(x\neq a)\tag{3}\]
Therefore,
\begin{align*}f'(a) &= \lim\limits_{x\rightarrow a} (x^{n-1} + x^{n-2}a + x^{n-3}a^2+\cdots+xa^{n-2}+a^{n-1})\\ &= a^{n-1} + a^{n-2}a + a^{n-3}a^2+\cdots+aa^{n-2}+a^{n-1}\quad(n\text{ terms})\\ &= na^{n-1}\end{align*}
This proves that \(f'(a) = na^{n-1}\), which we may also write as \(f'(x) = nx^{n-1}\).
Question 3.5 Derivative As a Function Progress Check 2
Find \(\dfrac{dy}{dx}\) for \(y=x^{17}\)
| A. |
| B. |
| C. |
CAUTION The Power Rule applies only to the power functions \(y = x^{n}\). It does not apply to exponential functions such as \(y = 2^{x}\). The derivative of \(y = 2^{x}\) is not \(x2^{x-1}\). We will study the derivatives of exponential functions later in this section.
We make a few remarks before proceeding:
- It may be helpful to remember the Power Rule in words: To differentiate \(x^{n}\), “bring down the exponent and subtract one (from the exponent).”
\[\frac{d}{dx}x^\text{exponent} = (\text{exponent})x^{\text{exponent}-1}\]
- The Power Rule is valid for all exponents, whether negative, fractional, or irrational:
\[\frac{d}{dx}x^{-\frac{3}{5}} = -\frac{3}{5}x^{-\frac{8}{5}}\text{ and } \frac{d}{dx}x^{\sqrt{2}}=\sqrt{2}x^{\sqrt{2}-1}\]
132
- The Power Rule can be applied with any variable, not just \(x\). For example,
\[\frac{d}{dz}z^2 = 2z,\;\frac{d}{dt}t^{20} = 20t^{19} \text{ and }\frac{d}{dr}r^{\frac{1}{2}} = \frac{1}{2}r^{-\frac{1}{2}}\]
Next, we state the Linearity Rules for derivatives, which are analogous to the linearity laws for limits.
THEOREM 2 Linearity Rules
Assume that \(f\) and \(g\) are differentiable. Then
Sum and Difference Rules: \(f + g\) and \(f - g\) are differentiable, and
\[(f+g)' = f' + g'\text{ and }(f-g)' = f' - g'\]
or, in Leibniz notation,
\[\frac{d}{dx} \left(f(x) + g(x)\right)= \frac{d}{dx} f(x) + \frac{d}{dx} g(x)\] and
\[\frac{d}{dx} \left(f(x) - g(x)\right)= \frac{d}{dx} f(x) - \frac{d}{dx} g(x)\]
Constant Multiple Rule: For any constant c, cf is differentiable and
\[(cf)' =cf'\]
or, in Leibniz notation,
\[\frac{d}{dx} \left(cf(x) \right)=c \frac{d}{dx} f(x)\]
Proof
To prove the Sum Rule, we use the definition
\[(f+g)'(x) = \lim\limits_{h\rightarrow 0}\frac{(f(x+h)+g(x+h))-(f(x)+g(x))}{h}\]
This difference quotient is equal to a sum \((h \neq 0)\):
\[\frac{(f(x+h)+g(x+h))-(f(x)-g(x))}{h}= \frac{f(x+h)-f(x)}{h} + \frac{g(x+h)-g(x)}{h}\]
Therefore, by the Sum Law for limits,
\begin{align*}(f+g)'(x) &= \lim\limits_{h\rightarrow 0}\frac{f(x+h)-f(x)}{h} + \lim\limits_{h\rightarrow 0}\frac{g(x+h)-g(x)}{h}\\[5pt] &= f'(x) + g'(x)\end{align*}
as claimed. The Difference and Constant Multiple Rules are proved similarly.
EXAMPLE 3
Find the points on the graph of \(f(t) = t^{3} - 12t + 4\) where the tangent line is horizontal (Figure 3.12).
Solution We calculate the derivative:
\begin{align*}\frac{df}{dt}&=\frac{d}{dt}(t^3-12t+4)\\ &=\frac{d}{dt}t^3 - \frac{d}{dt}(12t) + \frac{d}{dt}4 &&\text{(Sum and Difference Rules)}\\ &=\frac{d}{dt}t^3 - 12\frac{d}{dt}t + 0 &&\text{(Constant and Multiple Rules)}\\ &=3t^2-12&&\text{(Power Rule)}\end{align*}
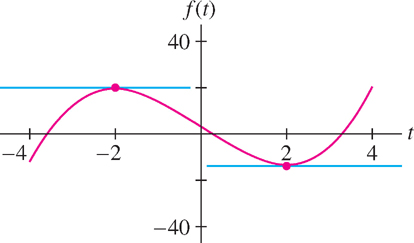
Note in the second line that the derivative of the constant 4 is zero. The tangent line is horizontal at points where the slope \(f'(t)\) is zero, so we solve
\[f'(t) = 3t^2-12=0\implies t=\pm 2\]
Now \(f(2) = -12\) and \(f(-2) = 20\). Hence, the tangent lines are horizontal at \((2, -12)\) and \((-2, 20)\).
133
EXAMPLE 4
Calculate \(\left.\frac{dg}{dt}\right|_{t=1}\), where \(g(t) = t^{-3}+2\sqrt{t} - t^{-\frac{4}{5}}\).
Solution We differentiate term-by-term using the Power Rule without justifying the intermediate steps. Writing \(\sqrt{t}\) as \(t^{\frac{1}{2}}\), we have
\begin{align*} \frac{dg}{dt} &= \frac{d}{dt}(t^{-3} + 2t^{\frac{1}{2}}-t^{-\frac{4}{5}})=-3t^{-4} + 2\left(\frac{1}{2}\right)t^{-\frac{1}{2}} - \left(-\frac{4}{5}\right)t^{-\frac{9}{5}}\\ &=-3t^{-4} + t^{-\frac{1}{2}} + \frac{4}{5}t^{-\frac{9}{5}}\\ \frac{dg}{dt}\Bigg|_{t=1} &=-3+1+\frac{4}{5} = -\frac{6}{5} \end{align*}
Question 3.6 Derivative As a Function Progress Check 3
Find the derivative \(f'(-1)\) for \(f(t)= 5t^3+2t^2-1\)
The derivative \(f'(x)\) gives us important information about the graph of \(f(x)\). For example, the sign of \(f'(x)\) tells us whether the tangent line has positive or negative slope, and the magnitude of \(f'(x)\) reveals how steep the slope is.
EXAMPLE 5 Graphical Insight
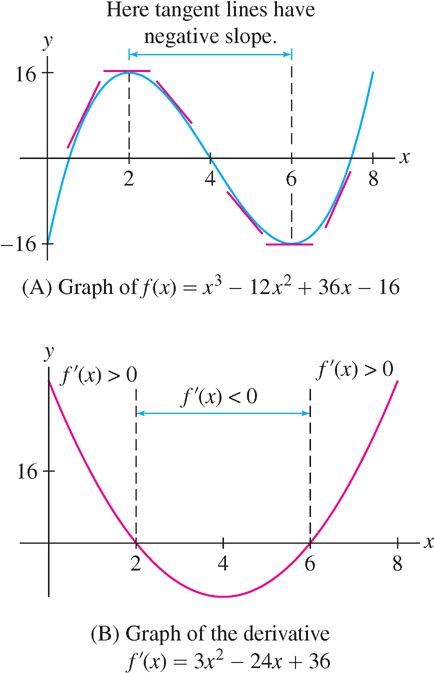
How is the graph of \(f(x) = x^{3} - 12x^{2} + 36x - 16\) related to the derivative \(f'(x) = 3x^{2} - 24x + 36\)?
Solution The derivative \(f'(x) = 3x^{2} - 24x + 36 = 3(x - 6)(x- 2)\) is negative for \(2 < x < 6\) and positive elsewhere (Figure 3.13B). The following table summarizes this sign information(Figure 3.13A):
| Property of \(f'(x)\) | Property of the Graph of \(f(x)\) |
|---|---|
| \(f'(x) < 0\) for \(2 < x < 6\) | Tangent line has negative slope for \(2 < x < 6\). |
| \(f'(2) = f'(6) = 0\) | Tangent line is horizontal at \(x = 2\) and \(x = 6\). |
| \(f'(x) > 0\) for \(x < 2\) and \(x > 6\) | Tangent line has positive slope for \(x < 2\) and \(x > 6\). |
Note also that \(f'(x)\rightarrow\infty\) as \(|x|\) becomes large. This corresponds to the fact that the tangent lines to the graph of \(f(x)\) get steeper as \(|x|\) grows large.
EXAMPLE 6 Identifying the Derivative
The graph of \(f(x)\) is shown in Figure 3.14(A). Which graph (B) or (C), is the graph of \(f'(x)\)?
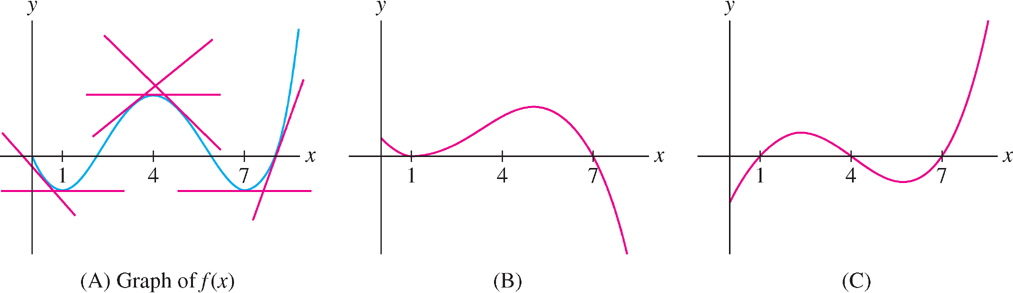
| Slope of Tangent Line | Where |
|---|---|
| Negative | \((0, 1)\) and \((4, 7)\) |
| Zero | \(x = 1, 4, 7\) |
| Positive | \((1, 4)\) and \((7, \infty)\) |
Solution In Figure 3.14(A) we see that the tangent lines to the graph have negative slope on the intervals \((0, 1)\) and \((4, 7)\). Therefore \(f'(x)\) is negative on these intervals. Similarly (see the table in the margin), the tangent lines have positive slope (and \(f'(x)\) is positive) on the intervals \((1, 4)\) and \((7, \infty)\). Only (C) has these properties, so (C) is the graph of \(f'(x)\).
134
3.2.2 The Number e: A Story of Mathematical Discovery
The logarithm function (or simply, the logarithm) was discovered by Scotsman John Napier (1550-1617) and Jobst Bürgi (1552-1632) from Switzerland in the sixteenth century and soon thereafter simplified by the English mathematician Henry Briggs (1561-1631) who introduced base 10. In his "Arithmetica Logarithmica" (1625), he introduced the first logarithm tables. The scientific impact of this work cannot be understated, leading quickly to the invention of the slide rule (a calculating device used in schools well into the 1960's) and Briggs' tables were instrumental to the work of astronomers like Johannes Kepler (1571-1630), who came across logarithms around 1616 and it was Kepler who first considered logarithms as functions.
Since logarithms allow one to reduce multiplication to addition and division to subtraction, namely
\[\log_{10} (AB) = \log_{10}A + \log_{10} B\]
\[\log_{10} (\frac{A}{B}) = \log_{10}A - \log_{10} B\]
for positive \(A\) and \(B\), difficult calculations with very large numbers become possible.
One should also note that, at the time, the Indian system of numeration using 0,1,2,..,9 (known also as the Arabic system) had not yet really taken hold in Europe.
Leonhard Euler (1707-1783), (Figure 3.15), was the greatest mathematician of the eighteenth century.

He was born in Basel, Switzerland, and studied under Johann Bernoulli. Euler contributed to many fields of mathematics and engineering, including calculus, number theory and was a founder of the fields of topology and the calculus of variations.
In the year 1728, when Euler was only 21, he wrote a scientific paper titled "Meditation Upon Experiments Made Recently on the Firing of a Canon." This paper was only published in 1862 in Euler's Opera Posthuma II. In this paper he introduces, for the first time, the number \(e \approx 2.71828\), and states that this number is that for which the logarithm is one. The letter \(e\) was again introduced by Euler in a letter (1731) to the mathematician Christian Goldbach.
Euler defines \(e\) as the limiting value of the numbers as \(n\) gets larger and larger, but did not prove that this limiting value existed (perhaps it was obvious to a genius of his magnitude.) Moreover, it is not clear to us how he actually arrived at this number. The important point we wish to make is that the existence of this incredible number is most assuredly not the result of a sudden burst of inspiration, but the result of seeking the answer to a natural question. We present here a likely scenario.
In the middle of the seventeenth century the Flemish mathematician Gregory of St. Vincent and the English mathematician Nicholas Mercator (not to be confused with the Flemish geographer Gerardus Mercator, who lived about a century earlier) independently discovered something remarkable. He considered the area under the hyperbola \(y=\frac{1}{t}\) from 1 to \(x\) and denoted this area as a function of \(x\), namely \(l(x)\).(see Figure 3.16)

Mercator discovered that the function had all the "properties" of a logarithm function which had earlier been pointed out by Kepler, namely
(i) \(l(xy)=l(x)+l(y)\)
(ii) \(l(\frac{x}{y})=l(x)-l(y)\)
(iii) \(l(x^r)=r l(x)\)
Since this logarithm arose as the area under a hyperbola, it was called "hyperbolic logarithm", or "natural logarithm", and only much later (in 1893) denoted by \(\ln (x)\).
But if \(l(x)=\ln(x)\) was a logarithm, there must be a base \(b\); i.e. a number \(b\) such that \(ln(b) = 1\) (Thus the area under \(y=\frac{1}{t}\) from 1 to \(b\) would also be 1.)
The question was, "what is \(b\)"? What was clear to Euler was the fact that \(\frac{d}{dx} \ln(x)=\frac{1}{x}\). This follows from the "Fundamental Theorem of Calculus" which will be studied in Calculus II.
Paraphrasing then the question Euler needed answered: For what number \(b\) is
\(\frac{d}{dx}\log_b (x) = \frac{1}{x}\) ?
To do this Euler needed a formula for this derivative.
As a student of the Swiss mathematician Johann Bernoulli, who was the author of the first ever calculus book, Euler became a master of this new discipline.
So let us, as Euler likely did, find this derivative from the definition:
\begin{eqnarray} \frac{dy}{dx} & = & \lim \limits_{h \longrightarrow 0} \frac{f(x+h)-f(x)}{h} \\ & = & \lim \limits_{h \longrightarrow 0} \frac{1}{h} \Big(\log_{b} (x+h)- \log_{b}(x) \Big) \\ & = & \lim \limits_{h \longrightarrow 0} \frac{1}{h} \Big(\log_{b} (\frac{x+h}{x}) \Big) \\ & = & \lim \limits_{h \longrightarrow 0} \frac{1}{h} \Big(\log_{b} (1+\frac{h}{x}) \Big) \\ & = & \lim \limits_{h \longrightarrow 0} \frac{1}{x} \Big(\frac{x}{h} \cdot \log_{b} (1+\frac{h}{x}) \Big) \\ & = & \lim \limits_{h \longrightarrow 0} \frac{1}{x} \log_{b} (1+\frac{h}{x})^\frac{x}{h} \\ & = & \frac{1}{x} \cdot \lim \limits_{h \longrightarrow 0} \log_{b} (1+\frac{h}{x})^\frac{x}{h} \end{eqnarray}
Here we must consider taking \(h\) small, but either positive or negative. Let us set \(h=\frac{x}{n}\) or \(h=-\frac{x}{n}\). Then the expression \((1+\frac{h}{x})^\frac{x}{h}\) becomes either \((1+\frac{1}{n})^n\) or \((1-\frac{1}{n})^{-n}\). It turns out that, as \(n\) gets larger and larger (\(n \longrightarrow \infty\)), both of these expressions get closer and closer to the same number, which Euler called \(e\) (for Euler?). We show first that the numbers \(e_n := (1+\frac{1}{n})^n\) get closer to some number (called \(e\)) as \(n\) gets larger. This is the claim that Euler makes in his 1728 paper, when he introduces the expression \((1+\frac{1}{n})^n\). From the binomial theorem one can show two facts:
- if \(n > m\), then \(e_n > e_m\)
- \(e_n < 3\) for all \(n\)
Thus, as \(n\) gets larger, the numbers \(e_n\) are moving to the right on the real number line (see Figure 3.17) yet must always stay to the left of the number 3.
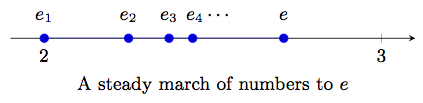
A very deep property of the real numbers asserts that there must be a real number \(e\) such that \(e_n\) gets arbitrarily close to \(e\) as \(n\) gets larger. We write this as: \[\lim \limits_{n \longrightarrow \infty} e_n = e\] Thus in the process of finding the derivative of \(y=\log_b x\), we (or Euler) discovered a totally new number \(e\). Before we proceed, we should show that
\[\lim \limits_{n \longrightarrow \infty} \big(1-\frac{1}{n}\big)^{-n}=\lim \limits_{n \longrightarrow \infty} \big(1+\frac{1}{n}\big)^{n}\]
For a video of a proof of this fact, click here.
Thus we may conclude that if \(y= \log_{b}x\), then
\[\frac{dy}{dx}=\frac{1}{x} \cdot \lim \limits_{h \longrightarrow 0} \log_{b} (1+\frac{h}{x})^\frac{x}{h}\]
= \(\frac{1}{x} \log_b e\) (by continuity). Hence, if \(b=e\), \[\frac{dy}{dx} = \frac{1}{x}\]
And: \(e\) was born !!
Having discovered \(e\), we now move on to the function
\[y=g(x)=e^x\]
We sketch a proof (arguing loosely as Euler often did) that
\[\frac{dy}{dx}= g^\prime(x)=e^x\]
that is, the function \(e^x\) is indestructible under differentiation. We proceed as follows:
\[\begin{eqnarray} \frac{dy}{dx} & = & \lim \limits_{h \longrightarrow 0} \frac{g(x+h)-g(x)}{h} \\ & = & \lim \limits_{h \longrightarrow 0} \frac{e^{x+h}-e^x}{h} \\ & = & \lim \limits_{h \longrightarrow 0} \frac{e^x(e^{h}-1)}{h} \\ & = & e^x \lim \limits_{h \longrightarrow 0} \frac{e^{h}-1}{h} \\ \end{eqnarray}\]
and from the definition of e this equals
\[e^x \lim \limits_{h \longrightarrow 0} \Big(\frac{\Big(\lim \limits_{n \longrightarrow \infty} \big(1+\frac{1}{n}\big)^{n}\Big)^{h}-1}{h}\Big)\]
We now argue loosely that we can interchange limits and parentheses (this may not have bothered mathematicians in the eighteenth century) to conclude that this is equal to
\[e^x \lim \limits_{h \longrightarrow 0} \lim \limits_{n \longrightarrow \infty} \Big(\frac{\big(1+\frac{1}{n}\big)^{nh}-1}{h}\Big)\]
and if these limits exist, it does not matter on how h goes to zero. So let us take \(h=\frac{1}{n}\). Then \(h \longrightarrow 0\) as \(n \longrightarrow \infty\) and we can simply write the above expression as
\[\begin{eqnarray} e^x \lim \limits_{n \longrightarrow \infty} \Big(\frac{\big(1+\frac{1}{n}\big)-1}{\frac{1}{n}}\Big) & = & e^x \lim \limits_{n \longrightarrow \infty} (1) \\ & = & e^x \\ \end{eqnarray}\]
Thus
\[\frac{d}{dx}e^x=e^x\]
We will give another derivation of this important formula in section 3.9. Euler subsequently showed that \(e\) is not a rational number and discovered an amazing connection between the numbers \(e, \pi\), and \(i\).
For a video to shed light on this amazing and surprising connection, click here (to be done).
The number \(e\) was introduced informally in Section 1.6. Now that we have the derivative in our arsenal, we can define \(e\) as follows: \(e\) is the unique number for which the exponential function \(f(x) = e^{x}\) is its own derivative. To justify this definition, we must prove that a number with this property exists. Let us summarize what we have shown as:
In some ways, the number \(e\) is “complicated”: It is irrational and it cannot be defined without using limits. However, the elegant formula \(\frac{d}{dx}e^x = e^x\) shows that \(e\) is “simple” from the point of view of calculus and that \(e^{x}\) is simpler than the seemingly more natural exponential functions \(2^{x}\) and \(10^{x}\).
THEOREM 3 The Number \(e\)
There is a unique positive real number \(e\) with the property
\[\frac{d}{dx}e^x = e^x\tag{4}\] \[\frac{d}{dx}\log_e x = \frac{d}{dx} \ln x = \frac{1}{x}\tag{5}\]
The number \(e\) is irrational, with approximate value \(e \approx 2.718\).
135
In many books, \(e^{x}\) is denoted \(\exp(x)\). Whenever we refer to the exponential function without specifying the base, the reference is to \(f(x) = e^{x}\). The number \(e\) has been computed to an accuracy of more than 100 billion digits. To 20 places,
\[e = 2.71828182845904523536\ldots\]
EXAMPLE 7
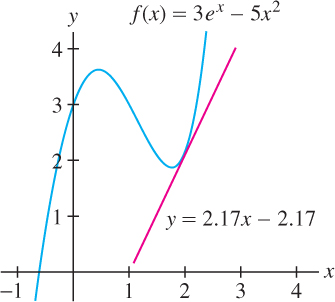
Find the tangent line to the graph of \(f(x) = 3e^{x} - 5x^{2}\) at \(x = 2\).
Solution We compute both \(f(2)\) and \(f(2)\):
\begin{align*}f'(x)&=\frac{d}{dx}(3e^x-5x^2)=3\frac{d}{dx}e^x - 5\frac{d}{dx}x^2 = 3e^x - 10x\\ f'(2)&=3e^2 - 10(2) \approx 2.17\\ f(2)&=3e^2-5(2^2) \approx2.17\end{align*}
An equation of the tangent line is \(y = f(2) + f'(2)(x - 2)\). Using these approximate values, we write the equation as (Figure 3.20)
\[y=2.17 + 2.17(x-2) \text{ or } y = 2.17x - 2.17\]
CONCEPTUAL INSIGHT
What precisely do we mean by \(b^{x}\) for any number \(b>0\)? We have taken for granted that \(b^{x}\) is meaningful for all real numbers \(x\) and all positive real numbers \(b\), but we never specified how \(b^{x}\) is defined. If \(n\) is a whole number, \(b^{n}\) is simply the product \(b\cdot b\cdots b\) (\(n\) times), and for any rational number \(x = \frac{m}{n}\),
\[b^x=b^{\frac{m}{n}}=\left(b^{\frac{1}{n}}\right)^m = \left(\sqrt[n]{b}\right)^m\]
When \(x\) is irrational, this definition does not apply and \(b^{x}\) cannot be defined directly in terms of roots and powers of \(b\). However, it makes sense to view \(b^{\frac{m}{n}}\) as an approximation to \(b^{x}\) when \(\frac{m}{n}\) is a rational number close to \(x\). For example, \(3^{\sqrt{2}}\) should be approximately equal to \(3^{1.4142} \approx 4.729\) because \(1.4142\) is a good rational approximation to \(\sqrt{2}\). Formally, then, we may define \(b^{x}\) as a limit over rational numbers \(\frac{m}{n}\) approaching \(x\):
\[b^x = \lim\limits_{\frac{m}{n}\rightarrow x}b^{\frac{m}{n}}\]
We can show that this limit exists and that the function \(f(x) = b^{x}\) thus defined is not only continuous but also differentiable (see Exercise 80 in Section 5.7). In Section 3.9 we derive a formula for the derivative of \(y= b^x\).
136
3.2.3 Differentiability, Continuity, and Local Linearity
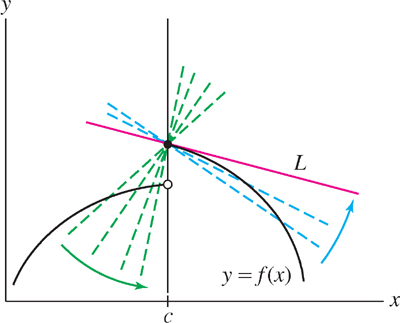
In the rest of this section, we examine the concept of differentiability more closely. We begin by proving that a differentiable function is necessarily continuous. In particular, a differentiable function cannot have any jumps. Figure 3.21 shows why: Although the secant lines from the right approach the line \(L\) (which is tangent to the right half of the graph), the secant lines from the left approach the vertical (and their slopes tend to \infty).
THEOREM 4 Differentiability Implies Continuity
If \(f\) is differentiable at \(x = c\), then \(f\) is continuous at \(x = c\).
Proof
By definition, if \(f\) is differentiable at \(x = c\), then the following limit exists:
\[f'(c) = \lim\limits_{x\rightarrow c}\frac{f(x) - f(c)}{x-c}\]
We must prove that \(\lim\limits_{x\rightarrow c}f(x)=f(c)\), because this is the definition of continuity at \(x = c\). To relate the two limits, consider the equation (valid for \(x \neq c\))
\[f(x) - f(c) = (x-c)\frac{f(x) - f(c)}{x-c}\]
Both factors on the right approach a limit as \(x \rightarrow c\), so
\begin{align*}\lim\limits_{x\rightarrow c}(f(x) - f(c)) &= \lim\limits_{x\rightarrow c}\left((x-c)\frac{f(x) - f(c)}{x-c}\right)\\ &=\left(\lim\limits_{x\rightarrow c}(x-c)\right)\left(\lim\limits_{x\rightarrow c}\frac{f(x) - f(c)}{x-c}\right)\\ &=0\cdot f'(c) = 0\end{align*}
by the Product Law for limits. The Sum Law now yields the desired conclusion:
\[\lim\limits_{x\rightarrow c}f(x) = \lim\limits_{x\rightarrow c}(f(x) - f(c)) + \lim\limits_{x\rightarrow c}f(c)=0+f(c)=f(c)\]
Most of the functions encountered in this text are differentiable, but exceptions exist, as the next example shows.
All differentiable functions are continuous by Theorem 4, but Example 9 shows that the converse is false. A continuous function is not necessarily differentiable.
EXAMPLE 9 Continuous But Not Differentiable
Show that \(f(x) = |x|\) is continuous but not differentiable at \(x = 0\).
Solution The function \(f(x)\) is continuous at \(x = 0\) because \(\lim\limits_{x\rightarrow 0}|x| = 0 = f(0)\). On the other hand,
\[f'(0) = \lim\limits_{h\rightarrow 0}\frac{f(0+h) - f(0)}{h}= \lim\limits_{h\rightarrow 0}\frac{|0+h| - |0|}{h} = \lim\limits_{h\rightarrow 0}\frac{|h|}{h}\]
This limit does not exist [and hence \(f(x)\) is not differentiable at \(x = 0\)] because
\[\frac{|h|}{h}=\begin{cases}1 & \text{if }h>0 \\-1 & \text{if }h<0 \end{cases}\]
and thus the one-sided limits are not equal:
\[\lim\limits_{h\rightarrow 0^+}\frac{|h|}{h}=1\text{ and }\lim\limits_{h\rightarrow 0^-}\frac{|h|}{h}=-1\]
137
GRAPHICAL INSIGHT
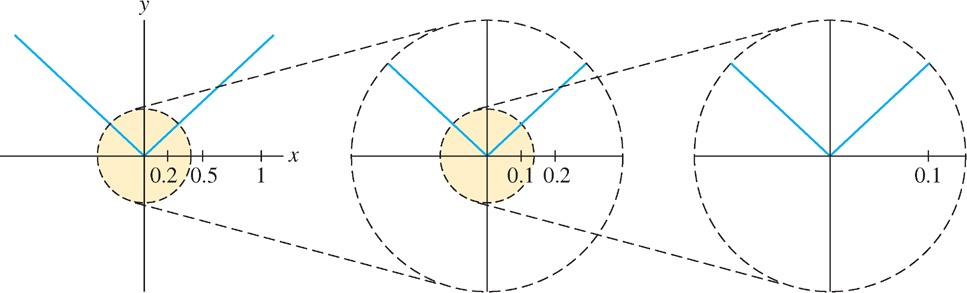
Differentiability has an important graphical interpretation in terms of local linearity. We say that \(f\) is locally linear at \(x = a\) if the graph looks more and more like a straight line as we zoom in on the point \((a, f(a))\). In this context, the adjective linear means “resembling a line,” and local indicates that we are concerned only with the behavior of the graph near \((a, f(a))\). The graph of a locally linear function may be very wavy or nonlinear, as in Figure 3.22. But as soon as we zoom in on a sufficiently small piece of the graph, it begins to appear straight.
Not only does the graph look like a line as we zoom in on a point, but as Figure 3.22 suggests, the “zoom line” is the tangent line. Thus, the relation between differentiability and local linearity can be expressed as follows:
- If \(f'(a)\) exists, then \(f\) is locally linear at \(x = a\): As we zoom in on the point \((a, f(a))\), the graph becomes nearly indistinguishable from its tangent line.
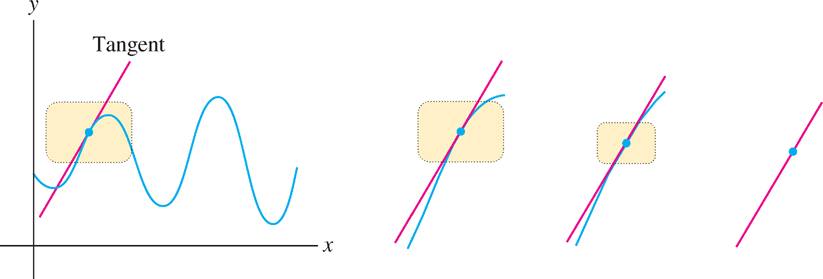
Local linearity gives us a graphical way to understand why \(f(x) = |x|\) is not differentiable at \(x = 0\) (as shown in Example 9). Figure 3.23 shows that the graph of \(f(x) = |x|\) has a corner at \(x = 0\), and this corner does not disappear, no matter how closely we zoom in on the origin. Since the graph does not straighten out under zooming, \(f(x)\) is not locally linear at \(x = 0\), and we cannot expect \(f'(0)\) to exist.
Another way that a continuous function can fail to be differentiable is if the tangent line exists but is vertical (in which case the slope of the tangent line is undefined).
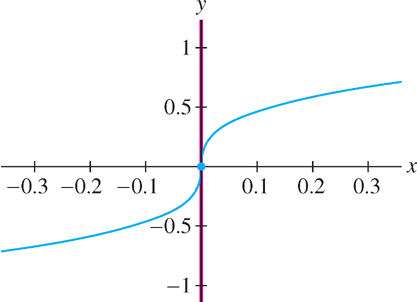
EXAMPLE 10 Vertical Tangents
Show that \(f(x) = x^{\frac{1}{3}}\) is not differentiable at \(x = 0\).
Solution The limit defining \(f'(0)\) is infinite:
\[\lim\limits_{h\rightarrow 0}\frac{f(h)-f(0)}{h} = \lim\limits_{h\rightarrow 0}\frac{h^{\frac{1}{3}}-0}{h} = \lim\limits_{h\rightarrow 0}\frac{h^{\frac{1}{3}}}{h}= \lim\limits_{h\rightarrow 0}\frac{1}{h^{{2}/{3}}}=\infty\]
Therefore, \(f'(0)\) does not exist (Figure 3.24).
138
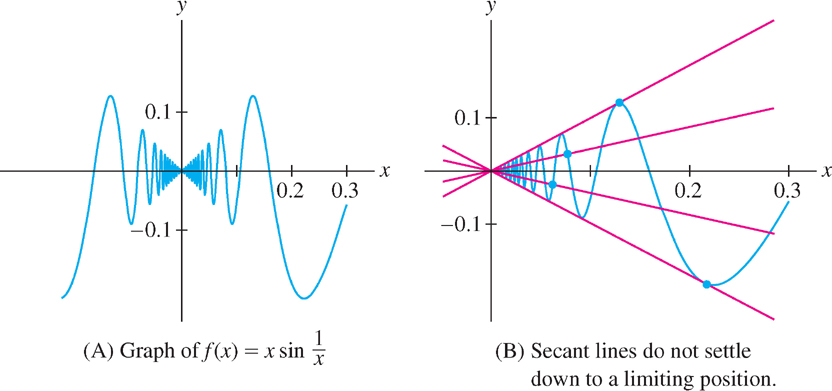
As a final remark, we mention that there are more complicated ways in which a continuous function can fail to be differentiable. Figure 3.25 shows the graph of \(f(x)=x\sin\frac{1}{x}\). If we define \(f(0) = 0\), then \(f\) is continuous but not differentiable at \(x = 0\). The secant lines keep oscillating and never settle down to a limiting position (see Exercise 97).
3.2.4 Section 3.2 Summary
- The derivative \(f'(x)\) is the function whose value at \(x = a\) is the derivative \(f'(a)\).
- We have several different notations for the derivative of \(y = f(x)\):
\[y',y'(x),f'(x),\frac{dy}{dx},\frac{df}{dx}\]
The value of the derivative at \(x = a\) is written
\[y'(a),f'(a),\frac{dy}{dx}\Bigg|_{x=a},\frac{df}{dx}\Bigg|_{x=a}\]
- The Power Rule holds for all exponents \(n\):
\[\frac{d}{dx}x^n = nx^{n-1}\]
- The Linearity Rules allow us to differentiate term by term:
\[\text{Sum Rule: }(f+g)'=f'+g'\text{, Constant Multiple Rule: }(cf)' = cf'\]
- The number \(e \approx 2.718\) is defined by the property \(m(e) = 1\), so that
\[\frac{d}{dx}e^x = e^x\]
- Differentiability implies continuity: If \(f(x)\) is differentiable at \(x = a\), then \(f(x)\) is continuous at \(x = a\). However, there exist continuous functions that are not differentiable.
- If \(f'(a)\) exists, then \(f\) is locally linear in the following sense: As we zoom in on the point \((a, f(a))\), the graph becomes nearly indistinguishable from its tangent line.
139